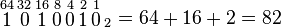Operaciones Con Números Binarios

Adición de números binarios.

La tabla de sumar para números binarios es la siguiente:

+	0	1
0	0	1
1	1	10

Las posibles combinaciones al sumar dos bits son:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10

Note que al sumar 1 + 1 es 102, es decir, llevamos 1 a la siguiente posición de la izquierda (acarreo). Esto es equivalente en el sistema decimal a sumar 9 + 1, que da 10: cero en la posición que estamos sumando y un 1 de acarreo a la siguiente posición.
Ejemplo

110011000 +

00010101 

——————————— 

10101101

Se puede convertir la operación binaria en una operación decimal, resolver la decimal, y después transformar el resultado en un (número) binario. Operamos como en el sistema decimal: comenzamos a sumar desde la derecha, en nuestro ejemplo, 1 + 1 = 10, entonces escribimos 0 en la fila del resultado y llevamos 1 (este "1" se llama acarreo o arrastre). A continuación se suma el acarreo a la siguiente columna: 1 + 0 + 0 = 1, y seguimos hasta terminar todas las columnas (exactamente como en decimal).
Sustracción de números binarios.

El algoritmo de la resta en sistema binario es el mismo que en el sistema decimal. Pero conviene repasar la operación de restar en decimal para comprender la operación binaria, que es más sencilla. Los términos que intervienen en la resta se llaman minuendo, sustraendo y diferencia.

Las restas básicas 0 - 0, 1 - 0 y 1 - 1 son evidentes:

0 - 0 = 0

1 - 0 = 1

1 - 1 = 0

0 - 1 = 1 (se transforma en 10 - 1 = 1) (en sistema decimal equivale a 2 - 1 = 1)

La resta 0 - 1 se resuelve igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 0 - 1 = 1 y me llevo 1 (este valor se resta al resultado que obtenga, entre el minuendo y el sustraendo de la siguiente columna), lo que equivale a decir en el sistema decimal, 2 - 1 = 1.
Ejemplos 

        10001                           11011001    
       -01010                          -10101011
       ——————                          —————————
        00111                           00101110 

En sistema decimal sería: 17 - 10 = 7 y 217 - 171 = 46.

Para simplificar las restas y reducir la posibilidad de cometer errores hay varios métodos:
Dividir los números largos en grupos. En el siguiente ejemplo, vemos cómo se divide una resta larga en tres restas cortas:

        100110011101             1001     1001     1101
       -010101110010            -0101    -0111    -0010
       —————————————      =     —————    —————    —————
        010000101011             0100     0010     1011

Producto de números binarios.

La tabla de multiplicar para números binarios es la siguiente:

·	0	1
0	0	0
1	0	1

El algoritmo del producto en binario es igual que en números decimales; aunque se lleva a cabo con más sencillez, ya que el 0 multiplicado por cualquier número da 0, y el 1 es el elemento neutro del producto.
Por ejemplo, multipliquemos 10110 por 1001:

        10110       
       x 1001                    
    —————————          
        10110               
       00000                
      00000                
     10110                
    —————————           
     11000110

En sistemas electrónicos, donde suelen usarse números mayores, se utiliza el método llamado algoritmo de Booth.

                 11101111
                 x 111011
                __________
                 11101111
                11101111
               00000000
              11101111
             11101111
            11101111
           ______________
           11011100010101

División de números binarios.
La división en binario es similar a la decimal; la única diferencia es que a la hora de hacer las restas, dentro de la división, estas deben ser realizadas en binario. Ejemplo

Dividir 100010010 (274) entre 1101 (13):

 100010010 /1101 = 010101
 -0000       
———————
 10001
 -1101
———————
  01000
 - 0000
 ———————
   10000
  - 1101
  ———————
    00111
   - 0000
   ———————
     01110
    - 1101
    ———————
     00001

Read More

Conversión Binario, Octal y Hexadecimal

Existe la posibilidad de convertir un binario en decimal.


El proceso para convertir un número del sistema binario al decimal es sencillo; basta con desarrollar el número, teniendo en cuenta el valor de cada dígito en su posición, que es el de una potencia de 2, cuyo exponente es 0 en el bit situado más a la derecha, y se incrementa en una unidad según vamos avanzando posiciones hacia la izquierda.

Por ejemplo, para convertir el número binario 10100112 a decimal, lo desarrollamos teniendo en cuenta el valor de cada bit:

1*26 + 0*25 + 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 83

10100112 = 8310
El número binario 1010010 corresponde en decimal al 82. Se puede representar de la siguiente manera:

entonces se suman los números 64, 16 y 2:

Para cambiar de binario con decimales a decimal se hace exactamente igual, salvo que la posición cero (en la que el dos es elevado a la cero) es la que está a la izquierda de la coma y se cuenta hacia la derecha a partir de -1:

Este proceso también pudiera ser al revez, convertir un decimal a binario.
Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.

A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Este será el número binario que buscamos.

Ejemplo

Transformar el número decimal 131 en binario. El método es muy simple:

131 dividido entre 2 da 65 y el residuo es igual a 1
65 dividido entre 2 da 32 y el residuo es igual a 1
32 dividido entre 2 da 16 y el residuo es igual a 0
16 dividido entre 2 da 8 y el residuo es igual a 0
8 dividido entre 2 da 4 y el residuo es igual a 0
4 dividido entre 2 da 2 y el residuo es igual a 0
2 dividido entre 2 da 1 y el residuo es igual a 0
1 dividido entre 2 da 0 y el residuo es igual a 1 -> Ordenamos los residuos, del último al primero: 10000011

En sistema binario, 131 se escribe 10000011

Otra forma de conversión consiste en un método parecido a la factorización en números primos. Es relativamente fácil dividir cualquier número entre 2. Este método consiste también en divisiones sucesivas. Dependiendo de si el número es par o impar, colocaremos un cero o un uno en la columna de la derecha. Si es impar, le restamos uno y seguiremos dividiendo entre dos, hasta llegar a 1. Después solo nos queda tomar el último resultado de la columna izquierda y todos los de la columna de la derecha y ordenar los dígitos de abajo a arriba.

Ejemplo

100|0
50|0
25|1 --> 1, 25-1=24 y seguimos dividiendo entre 2
12|0
6|0
3|1
1|1 -


Decimal (con decimales) a binario.
Para transformar un número del sistema decimal al sistema binario:

Se transforma la parte entera a binario. (Si la parte entera es 0 en binario será 0, si la parte entera es 1 en binario será 1, si la parte entera es 5 en binario será 101 y así sucesivamente).

Se sigue con la parte fraccionaria, multiplicando cada número por 2. Si el resultado obtenido es mayor o igual a 1 se anota como un uno (1) binario. Si es menor que 1 se anota como un 0 binario. (Por ejemplo, al multiplicar 0.6 por 2 obtenemos como resultado 1.2 lo cual indica que nuestro resultado es un uno (1) en binario, sólo se toma la parte decimal del resultado).

Después de realizar cada multiplicación, se colocan los números obtenidos en el orden de su obtención.

Algunos números se transforman en dígitos periódicos, por ejemplo: el 0.1.
Ejemplo.

0,3125 (decimal) => 0,0101 (binario).
Proceso:
0,3125 * 2 = 0,625 => 0
0,625 * 2 = 1,25 => 1
0,25 * 2 = 0,5 => 0
0,5 * 2 = 1 => 1
En orden: 0101 -> 0,0101 (binario)

Ejemplo
0,1 (decimal) => 0,0 0011 0011 ... (binario).
Proceso:
0,1 * 2 = 0,2 ==> 0
0,2 * 2 = 0,4 ==> 0
0,4 * 2 = 0,8 ==> 0
0,8 * 2 = 1,6 ==> 1
0,6 * 2 = 1,2 ==> 1
0,2 * 2 = 0,4 ==> 0 <--se repiten las cuatro cifras, periódicamente
0,4 * 2 = 0,8 ==> 0 <- 0,8 * 2 = 1,6 ==> 1 <- 0,6 * 2 = 1,2 ==> 1 <- ...
En orden: 0 0011 0011 ... => 0,0 0011 0011 ... (binario periódico)

Binario a decimal (con parte fraccionaria binaria)
Inicie por el lado izquierdo (la primera cifra a la derecha de la coma), cada número deberá ser multiplicado por 2 elevado a la potencia consecutiva a la inversa (comenzando por la potencia -1, 2-1).

Después de realizar cada una de las multiplicaciones, sume todas y el número 
resultante será el equivalente al sistema decimal.
 Ejemplos
0,101001 (binario) = 0,640625(decimal).
Proceso:1 * 2 elevado a -1 = 0,5
0 * 2 elevado a -2 = 0
1 * 2 elevado a -3 = 0,125
0 * 2 elevado a -4 = 0
0 * 2 elevado a -5 = 0
1 * 2 elevado a -6 = 0,015625
La suma es: 0,640625

0,110111 (binario) = 0,859375(decimal).
Proceso:1 * 2 elevado a -1 = 0,5
1 * 2 elevado a -2 = 0,25
0 * 2 elevado a -3 = 0
1 * 2 elevado a -4 = 0,0625
1 * 2 elevado a -5 = 0,03125
1 * 2 elevado a -6 = 0,015625
La suma es: 0,859375

  
Conversión entre sistema binario y octal.
Debido a que el sistema octal tiene como base 8, que es la tercera potencia de 2, y que dos es la base del sistema binario, es posible establecer un método directo para convertir de la base dos a la base ocho, sin tener que convertir de binario a decimal y luego de decimal a octal. Este método se describe a continuación:

Para realizar la conversión de binario a octal, realice lo siguiente:
Agrupe la cantidad binaria en grupos de 3 en 3 iniciando por el lado derecho. Si al terminar de agrupar no completa 3 dígitos, entonces agregue ceros a la izquierda.

Posteriormente vea el valor que corresponde de acuerdo a la tabla:

Número en binario	000	001	010	011	100	101	110	111
Número en octal	0	1	2	3	4	5	6	7

La cantidad correspondiente en octal se agrupa de izquierda a derecha.
Ejemplos
110111 (binario) = 67 (octal). Proceso:
111 = 7
110 = 6
Agrupe de izquierda a derecha: 67
11001111 (binario) = 317 (octal). Proceso:
111 = 7
001 = 111 entonces agregue un cero, con lo que se obtiene 011 = 3
Agrupe de izquierda a derecha: 317

Si el número binario tiene parte decimal, se agrupa de tres en tres desde el punto decimal hacia la derecha siguiendo los mismos criterios establecidos anteriormente para números enteros. Por ejemplo:
0.01101 (binario) = 0.32 (octal) Proceso:
011 = 3 01 entonces Agregue 010 = 2 Agrupe de izquierda a derecha: 32 Agregue la parte entera: 0.32

Octal a binario.
Cada dígito octal se convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.
Ejemplo

El 2 en binario es 10, pero en binario de 3 bits es Oc(2) = B(010);
el Oc(4) = B(100) y el Oc(7) = (111),
luego el número en binario será 010100111.

Conversión entre binario y hexadecimal.
Para realizar la conversión de binario a hexadecimal, realice lo siguiente:
Agrupe la cantidad binaria en grupos de 4 en 4 iniciando por el lado derecho. Si al terminar de agrupar no completa 4 dígitos, entonces agregue ceros a la izquierda.

Posteriormente vea el valor que corresponde de acuerdo a la tabla:

Número en binario	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
Número en hexadecimal	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

La cantidad correspondiente en hexadecimal se agrupa de derecha a izquierda.
Ejemplos

110111010 (binario) = 1BA (hexadecimal).
Proceso:
1010 = A
1011 = B
1 entonces agregue 0001 = 1
Agrupe de derecha a izquierda: 1BA
11011110101 (binario) = 6F5 (hexadecimal).
Proceso:0101 = 5
1111 = F
110 entonces agregue 0110 = 6
Agrupe de derecha a izquierda: 6F5

Hexadecimal a binario.
Note que para pasar de Hexadecimal a binario, se reemplaza el número Hexadecimal por el equivalente de 4 bits, de forma similar a como se hace de octal a binario.
Tabla de conversión entre decimal, binario, hexadecimal, octal, BCD, Exceso 3 y Gray o Reflejado

Decimal	Binario	Hexadecimal	Octal	BCD	Exceso 3	Gray o Reflejado
0	0000	0	0	0000	0011	0000
1	0001	1	1	0001	0100	0001
2	0010	2	2	0010	0101	0011
3	0011	3	3	0011	0110	0010
4	0100	4	4	0100	0111	0110
5	0101	5	5	0101	1000	0111
6	0110	6	6	0110	1001	0101
7	0111	7	7	0111	1010	0100
8	1000	8	10	1000	1011	1100
9	1001	9	11	1001	1100	1101
10	1010	A	12	0001 0000		1111
11	1011	B	13	0001 0001		1110
12	1100	C	14	0001 0010		1010
13	1101	D	15	0001 0011		1011
14	1110	E	16	0001 0100		1001
15	1111	F	17	0001 0101		1000

Factorización.
Tabla de conversión entre binario, factor binario, hexadecimal, octal y decimal

Binario	Factor binario	Hexadecimal	Octal	Decimal
0000 0010	21	2	2	2
0000 0100	22	4	4	4
0000 1000	23	8	10	8
0001 0000	24	10	20	16
0010 0000	25	20	40	32
0100 0000	26	40	100	64
1000 0000	27	80	200	128

Read More

Sistema Binario.

¿Que es un Sistema Binario?

Antes de Saber que es un sistema binario te invito a comprender que es un sistema de numeración haciendo click en (sistema de numeración).


El sistema binario, llamado también sistema diádico en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente dos cifras: cero y uno (0 y 1). Es uno de los que se utilizan en las computadoras, debido a que estas trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).

¿Como se Representa en el Sistema Binario? 

En el sistema binario sólo se necesitan dos cifras.
En informática, un número binario puede ser representado por cualquier secuencia de bits (dígitos binarios), que suelen representar cualquier mecanismo capaz de usar dos estados mutuamente excluyentes. Las siguientes secuencias de símbolos podrían ser interpretadas como el mismo valor numérico binario:


1 0 1 0 0 1 1 0 1 1
¦ − ¦ − − ¦ ¦ − ¦ ¦
x o x o o x x o x x
y n y n n y y n y y

El valor numérico representado en cada caso depende del valor asignado a cada símbolo. En una computadora, los valores numéricos pueden representar dos voltajes diferentes; también pueden indicar polaridades magnéticas sobre un disco magnético. Un "positivo", "sí", o "sobre el estado" no es necesariamente el equivalente al valor numérico de uno; esto depende de la nomenclatura usada.


De acuerdo con la representación más habitual, que es usando números arábigos, los números binarios comúnmente son escritos usando los símbolos 0 y 1. Los números binarios se escriben a menudo con subíndices, prefijos o sufijos

para indicar su base. Las notaciones siguientes son equivalentes:

100101 binario (declaración explícita de formato)
100101b (un sufijo que indica formato binario)
100101B (un sufijo que indica formato binario)
bin 100101 (un prefijo que indica formato binario)
1001012 (un subíndice que indica base 2 (binaria) notación)
%100101 (un prefijo que indica formato binario)
0b100101 (un prefijo que indica formato binario, común en lenguajes de programación)

Read More